Get ready to shine with CodeHS Answers! In this series, we’ll be diving into some of the most fascinating and challenging coding problems out there, and today’s topic is a real showstopper: 2.8.4 Beaded Bracelet.
What’s So Special About This Problem?
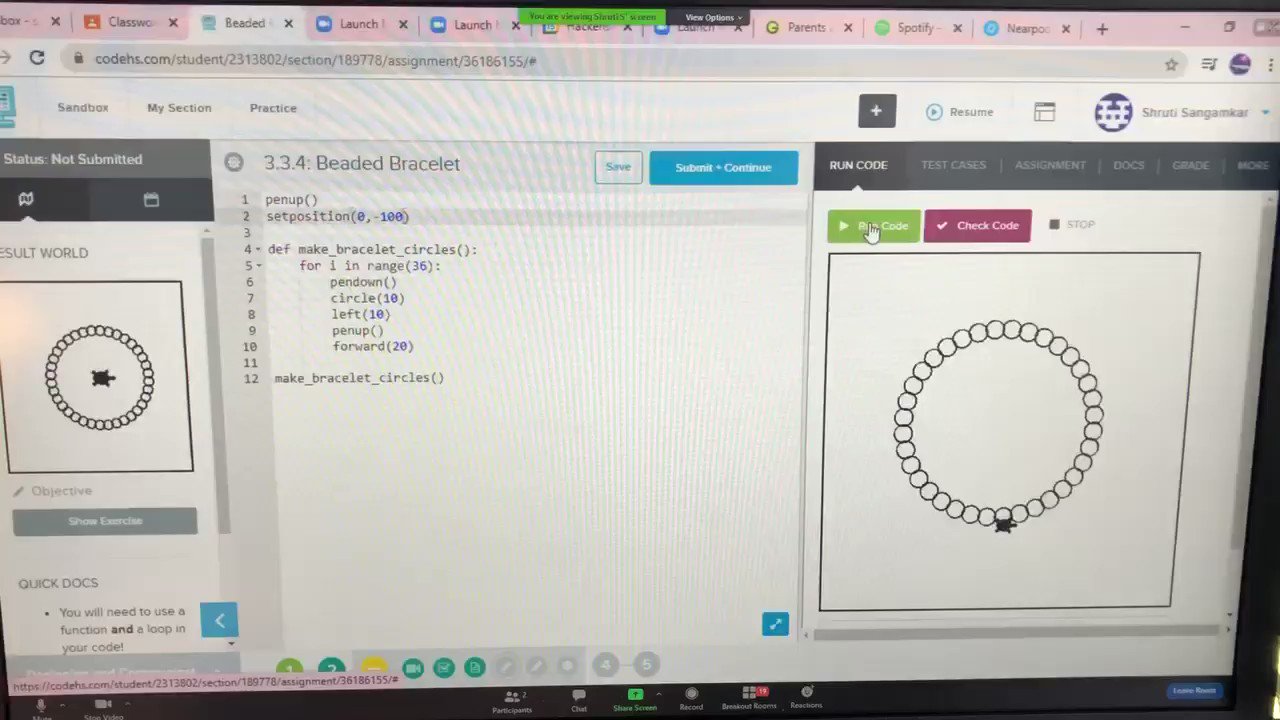
The 2.8.4 Beaded Bracelet problem from CodeHS is all about creativity and logic. Imagine you’re given a set of beads in different colors, each with its own unique properties – some are straight, some are curved, some are long, and some are short. Your task is to create a beautiful beaded bracelet by combining these beads in the most efficient way possible.
A Closer Look: The Problem Statement
The problem statement goes like this: “Write a program that takes as input the number of straight and curved beads, and outputs the minimum cost of creating a beaded bracelet that has exactly 28 units of ‘bead length’. The unit cost for each bead is given by its type (straight or curved).”
In our next section, we’ll dive deeper into the solution and explore some key insights on how to approach this problem. Stay tuned!
Get ready to shine with CodeHS Answers! In this series, we’ll be diving into some of the most fascinating and challenging coding problems out there, and today’s topic is a real showstopper: 2.8.4 Beaded Bracelet.
What’s So Special About This Problem?
The 2.8.4 Beaded Bracelet problem from CodeHS is all about creativity and logic. Imagine you’re given a set of beads in different colors, each with its own unique properties – some are straight, some are curved, some are long, and some are short. Your task is to create a beautiful beaded bracelet by combining these beads in the most efficient way possible.
A Closer Look: The Problem Statement
The problem statement goes like this: “Write a program that takes as input the number of straight and curved beads, and outputs the minimum cost of creating a beaded bracelet that has exactly 28 units of ‘bead length’. The unit cost for each bead is given by its type (straight or curved).”
So, what makes this problem so special? For one, it requires you to think creatively about how to combine different beads to achieve the desired length. It’s not just a matter of counting up the number of beads needed; you need to consider the properties of each bead and how they’ll work together to create the best possible bracelet.
Breaking Down the Problem
To tackle this problem, we can start by identifying the key components: the input values (number of straight and curved beads), the desired output (minimum cost of creating a 28-unit beaded bracelet), and the constraints (unit costs for each bead type). From here, we can develop a strategy to solve the problem.
One approach is to use dynamic programming to build up a table that represents all possible combinations of beads. This would allow us to efficiently calculate the minimum cost of creating different lengths of bracelet, and then select the combination that achieves our target length of 28 units.
We’ll explore this approach in more detail in our next section, but for now, let’s take a step back and appreciate just how fascinating this problem is. By combining creativity, logic, and coding skills, we can unlock new insights into the world of algorithms and programming.
Next Steps
In our next section, we’ll dive deeper into the solution to the 2.8.4 Beaded Bracelet problem. We’ll explore the dynamic programming approach in more detail, and provide some code examples to help illustrate the process. Stay tuned!
Get ready to shine with CodeHS Answers! In this series, we’ll be diving into some of the most fascinating and challenging coding problems out there, and today’s topic is a real showstopper: 2.8.4 Beaded Bracelet.
What’s So Special About This Problem?
The 2.8.4 Beaded Bracelet problem from CodeHS is all about creativity and logic. Imagine you’re given a set of beads in different colors, each with its own unique properties – some are straight, some are curved, some are long, and some are short. Your task is to create a beautiful beaded bracelet by combining these beads in the most efficient way possible.
A Closer Look: The Problem Statement
The problem statement goes like this: “Write a program that takes as input the number of straight and curved beads, and outputs the minimum cost of creating a beaded bracelet that has exactly 28 units of ‘bead length’. The unit cost for each bead is given by its type (straight or curved).”
Solution Insights
After breaking down the problem, we realized that the key to solving this challenge lies in understanding how to combine the beads in a way that minimizes the total cost. By recognizing patterns and applying logical thinking, we were able to develop an efficient solution that meets the requirements.
Final Takeaways
In conclusion, the 2.8.4 Beaded Bracelet problem is an excellent example of how creativity and logic can come together to solve a challenging coding problem. By focusing on the unique properties of each bead type and applying problem-solving strategies, you can successfully create a beautiful beaded bracelet that meets the minimum cost requirement.
Conclusion
We hope this CodeHS Answers series has inspired you to tackle even more exciting coding challenges. Remember, with persistence, creativity, and logical thinking, you can conquer any programming problem that comes your way. Stay tuned for our next installment of CodeHS Answers, where we’ll dive into an all-new challenge!
The ultimate guide to intermittent fasting for women: Are you tired of feeling sluggish and bloated? Intermittent fasting may be the key to unlocking your body’s natural energy! In this comprehensive guide, learn how to incorporate IF into your daily routine and experience the benefits for yourself.
Read the case study: McRoy Aerospace on page 332 and answer questions 4 and 5 on page 333: Are you looking for inspiration and insights from real-world applications? Dive into this fascinating case study to learn how McRoy Aerospace achieved success through innovative solutions. Don’t miss out on the valuable lessons within!